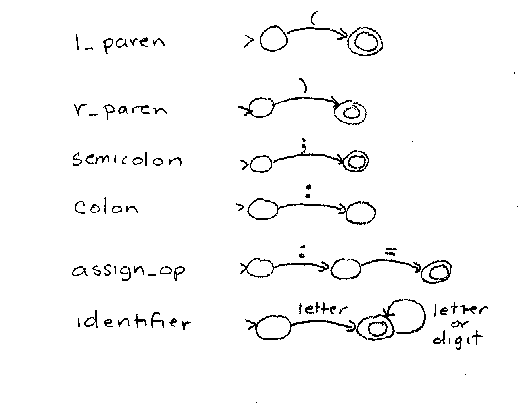
There are a number of steps to follow in implementing a scanner. Of course there are various choices to make at each step. We will look at one way in detail and mention others along the way. For consistency's sake, we will require that your projects be done the way presented here.
Use the ISO or other standard for the language to list all of the tokens in the language. Sometimes tokens are provided for you in the language definition. Other times they are not. Sometimes they are listed separately from the EBNF for the programming language, and sometimes not. If they are not, it makes it a little more difficult to extract the tokens from the other parts of the grammar in the EBNF form.
Example. In the EBNF for mPascal, identifier appears to be a nonterminal, because it appears on the left hand side of a rule. However, it is a token. Every variable name, as well as every keyword has the form of an identifier. The parser does not need to know the individual characters in an identifier to be able to complete its parse.
So, how can one determine what the tokens in a programming language are? Listing the tokens may take a little practice if there is no list given to you to start with. Essentially, anything you see when you look at the source text of a program is a token or part of a token. Essentially, a token is a piece of a program that you cannot further divide without losing its meaning.
For example, in the line
X35 := X35 - Aardvark;
there are six tokens. The first is X35. The three characters used--X, 3, and 5--form an identifier. It does not make sense to further subdivide this identifier into X or 35, because those strings have no meaning separately in this line. Furthermore, assignment operator
:=
is a token. Although the colon and the equals sign do have individual meanings in a Pascal program, in this context they together form the assignment operator and cannot be further subdivided. The next occurrence of X35 is also a new token (identifier), and the subtraction operator, the identifier Aardvark, and the final semicolon are each tokens. Tokens are easily picked out of the definition of a language with a little practice.
The regular expressions corresponding to the tokens of the language will often be provided for you as part of the EBNF definition of the programming language you are compiling. If they aren't, you will need to develop them yourself, as in this class. We do this to help you learn the correlation between tokens and regular expressions. Any standardized programming language would certainly have all of the tokens clearly defined..
Using the regular expression for each token, construct an equivalent finite state automaton for each token, as in:

In the theory of finite state automata, it is assumed that the finite state automaton will read the entire input string from start to finish. When the entire input is consumed, the automaton is examined to see which state it is in. If it is in an accept state, the input string is accepted; otherwise, it is rejected.
In scanning tokens in source code, this doesn't work, because we come to the end of the token before the end of the file in all but one case. So we have to modify the finite state automata to account for this fact. The best way to do this is to use formal assertions to direct the design process.
A precondition for each fsa could be
In our illustrations above, we can see that there will be a part of the scanner (which we might as well call by the descriptive name "dispatcher") that knows which finite state automaton to call given the first character of the next token. It would be up to the dispatcher to ensure that the precondition is met before calling any fsa.
A postcondition for each fsa could be
These pre and post conditions provide clear directions for the design of the dispatcher and the fsa's. For example, in order to make sure that the postcondition is satisfied, we would have to modify the above fsa's to show where to assign the token scanned, when to concatenate characters scanned with a lexeme variable, and how to reset the file pointer to the first character after the token scanned in cases where too many characters were read.
These individual finite state automata could be combined into a single nondeterministic finite state automaton by creating a new start state and connecting this new start state to the original start states of each original fsa by way of empty transitions:
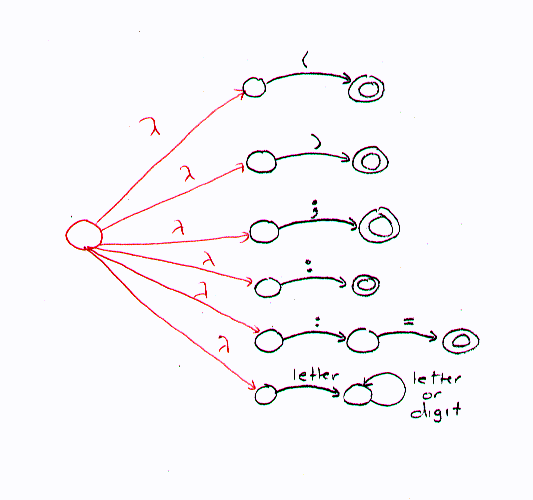
The theory of finite state automata tells us that for every nondeterministic fsa there is an equivalent deterministic fsa. That is, there is an algorithm that would turn the above nondeterministic fsa into an equivalent deterministic fsa. We wouldn't want to do this, however, because the single fsa for a real programming language scanner would be huge, unreadable, and difficult to maintain or modify. Instead, it is much better to have smaller, individual fsa's for each token that can be implemented as small, individual procedures. In this case, it is easy to insert a new token scanning component, remove others, and change existing ones. It also makes it easy to divide the project up among team members, as each member can take on a subset of the fsa's to implement.
That leaves a question, however: how can it be determined which fsa should be called when the scanner is invoked? One way is to build a "dispatcher." The dispatcher executes each time the scanner is called by the driver to get a new token. The dispatcher starts by skipping any white space in the input file until the first non white space character is encountered. The dispatcher then uses this non white space character (without removing it from the input file) to determine which fsa to call, as in:
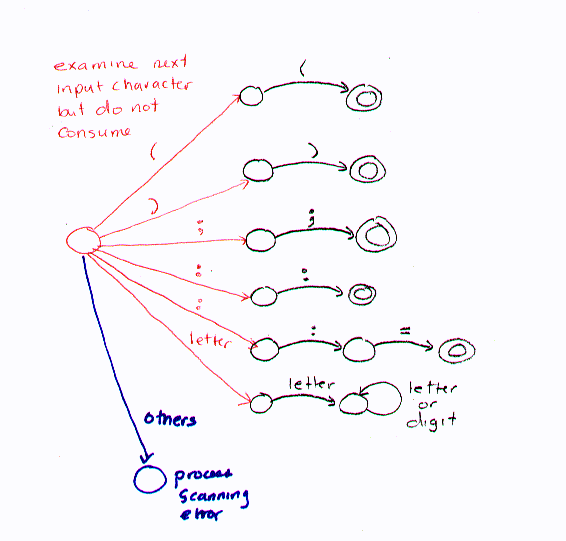
Notice that this diagram shows the situation of the dispatcher after white space has been skipped. Notice also the blue line. If the first non white space encountered is a character that can be the start of no token, we have a scanning error, which we will need to learn how to handle.
Some branches in the initial dispatcher might be nondeterministic, as in the two that are labeled with the colon above. These two branches lead to the two fsa's given below.
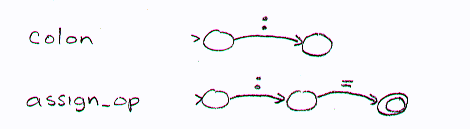
To remove the nondeterminism from the scanner, we can simply combine the fsa's into a single deterministic fsa (again, recall from the theory of fsa's that we can always find an equivalent deterministic version of any nondeterministic fsa. In this case, we would get the fsa below.
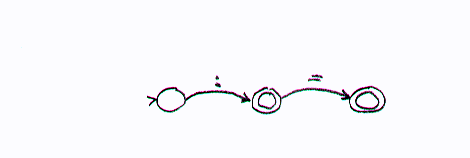
In addition to the inclusion of the dispatcher for deciding which fsa to call, we need to modify each fsa to deal with practical issues of scanning. The following diagram shows how the above fsa might be so modified:
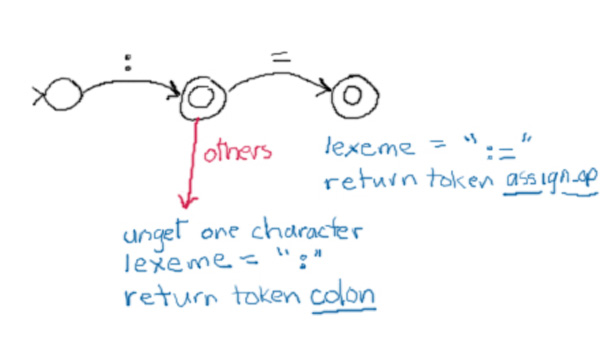
The others transition from the second state just means that if any other character than an = is encountered during scanning at this point, then the token we found was the colon, not the assignment operator. Thus we must have read one character too far. The fsa implementation must account for this by putting the extra character back into the file (noted here with the unget command). Other things the scanner must do include constructing the corresponding lexeme, keeping track of the current column number, and returning the token found.
The routine for skipping white space (the initial action taken by the dispatcher each time a new token is requested) is required to take care of the current line number. The reason is that the end of line character is considered a white space character, and thus will be encountered while skipping white space.
One good technique for developing large programs is the use of stubs. A stub is just a procedure, function, or method that will be needed but which is not yet completed. Putting a stub in a program helps organize the program. As a stub is completed, it can often be tested before all other stubs are finished. In this project, since every token must have a procedure or method that handles the pattern matching for the token, it is a wise idea to create stubs for each token in the scanner. A driver can then exercise each stub by calling it. The stub should just have enough code to indicate that it has been called successfully. An example is:
procedure Identifier; -- The token Identifier is matched in the input streambegin Output("Made it to token Identifier"); end;
This procedure is a stub for the identifier token handler. Eventually, the output statement will be replaced with the code for scanning an identifier.