We give here an example of symbol table construction. The approach is to build a new symbol table for each scope encountered, stacking new symbol tables on top of the old ones, and popping (destroying) symbol tables when a scope is left.
To understand what goes into symbol table construction, an example is warranted.
Consider the following program skeleton.
program Fred; var A, B, C : Integer;
procedure A1(A : in Integer);
var Q, X : Real;
Ch : Character;
function Snort(W : in Integer) return Integer;
var X : Integer;
begin -- Snort
X := A + C;
end Snort
begin -- A1
Write (Snort(C));
end A1;
procedure Sort(A : in out List; N in Integer);
begin
X := 4.5;
Sort(A, N/2);
end;
begin --Fred
Write(A, X);
end.
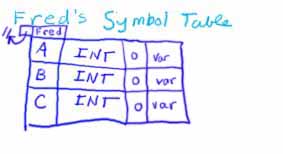
Look at the above program. As we start to parse, we encounter the three variables, A, B, and C in the declaration:
var A, B, C : Integer;
They should each be placed into Fred's symbol table, as shown.

At this point the parser encounters the declaration of procedure A1 in the line
procedure A1(A : in Integer);
The name of this procedure belongs in Fred's symbol table, along with its attributes. The attributes include the number, types, and modes of the parameters.
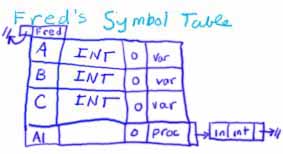
At this point, the parser drops into procedure A1 and begins parsing there. This procedure represents a new scope, and one good way to handle an new scope is to create a new symbol table for it. Following the example given in constructing Fred's symbol table, this yields the following.
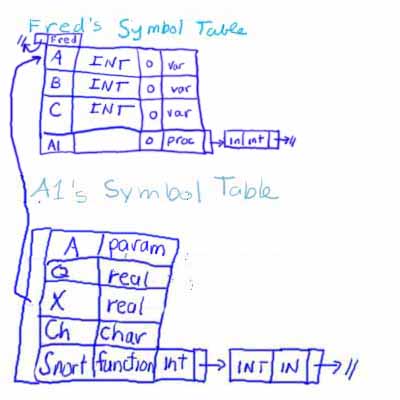
Notice that we have linked A1's symbol table to Fred's symbol table. This takes care of the fact that all identifiers inside A1 are in scope inside A1 as are all of the identifiers in Fred, unless the same identifier name is used in both scopes. In the latter case, the first identifier that matches, starting with the innermost scope and moving out (i.e., starting with the top of the stack and moving down) is used.
Now parsing begins inside Snort. Following the same procedure, we create a new symbol table for Snort, make that symbol table the top of stack symbol table, and link it with the containing scopes, as shown.
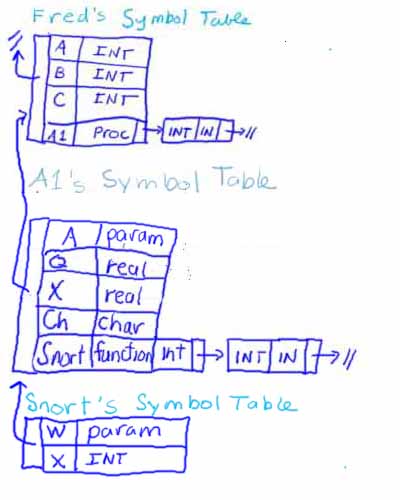
Inside Snort, we encounter the statement:
X := A + C;
Notice how each identifier is resolved. We look for X in Snort, and we find it. We look for A in snort, and we do not find it, so we follow the link to the next symbol table in scope and find A there. We then look for C in Snort's symbol table. We don't find it, so we follow the link to A1's symbol table, and we don't find it there either. So, we follow the link from A1's symbol table to Fred's symbol table, and we find C there. To successfully translate
X := A + C;
our program would need to be sure that all of the types are compatible with the operations to be performed (a topic to be covered later). If an identifier is not found in this search of scopes, it hasn't been declared and an error must be generated.
At this point we are done parsing function Snort. The action taken is to remove Snort's symbol table (i.e., pop it off the stack), because it is no longer needed. None of its identifiers will ever be in scope for any other part of the program. This leaves the symbol table structure looking like:

At this point, we begin parsing the body of procedure A1, where we encounter
Write (Snort(C));
Notice that identifier Snort is in A1's scope, so we can generate code to make the call to Snort. We would have to ensure that the actual parameter (C) is declared and of the right type for the type and mode of the formal parameter. We find C in scope in Fred's symbol table and see that it indeed is a proper match for the formal parameter of Snort, whose description we find in A1's symbol table.
Once we are done parsing the body of procedure A1, we pop its symbol table, leaving the symbol table structure looking like:

Another curious thing happens at this point. We encounter a new procedure declaration (procedure Sort) in Fred's scope. This means that we have to add a new entry for Sort in Fred's symbol table as well as a new symbol table for Sort, as shown below:
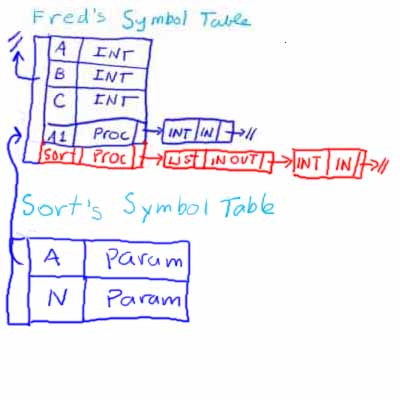
This should help us understand why we need prototypes. Even though by the end of the program, Sort is in Fred's scope, we don't encounter it until we reach Sort in our parse. This means that although procedure A1 should technically be able to call Sort, it can't, because when we are parsing A1, Sort is not in Fred's symbol table.
What if we had a situation in which A1 needed to call Sort and Sort needed to call A1? A solution to this problem would be to include a prototype of Sort early on, if the programming language allows it. That is, a statement similar to
prototype procedure Sort(A : in out List; N in Integer);
could be included in the same location where Fred's variables are declared. The compiler could put all of the necessary information into the symbol table for Sort at that point. Later, when the complete procedure for Sort is encountered, its body can be translated at that time.
Back to the situation we are in in our example, once the compilation of procedure Sort is completed, we can discard Sort's symbol table, leaving:
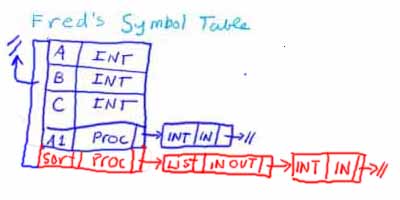
Now we can compile the body of Fred.
begin --Fred
Write(A, X);
end.
At this point the compiler would uncover an error. The variable X is not in Fred's symbol table, so the compiler would print a message similar to "Variable X on line 34, column 5 is undefined."
We have just completed a long walkthrough of how the symbol table structure would be constructed as an example program was parsed. The main things to note are: