
--> s=poly(0,'s');
--> str='(s-1)/(s^2-5*s+1)';
--> rep=x_dialog('Nominal plant?',str)
rep =
(s-1)/(s^2-5*s+1)
--> if rep==[] then return,end
--> Plant=evstr(rep);
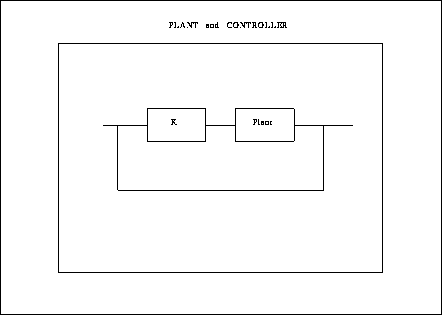
--> Plant=syslin('c',Plant);
-->
-->//Nominal Plant
-->P22=tf2ss(Plant); //...in state-space form
-->[ny,nu,nx]=size(P22);
-->x_message('Now enter weighting matrices');
Now enter weighting matrices
-->rep=x_matrix('x-weighting matrix',eye(nx,nx))
rep =
! 1. 0. !
! 0. 1. !
-->if rep==[] then return,end
-->Qx=evstr(rep);
-->rep=x_matrix('u-weighting matrix',eye(nu,nu));
-->if rep==[] then return,end
-->Qu=evstr(rep);
-->bigQ=sysdiag(Qx,Qu);
-->rep=x_matrix('x-noise covariance matrix',eye(nx,nx))
rep =
! 1. 0. !
! 0. 1. !
-->if rep==[] then return,end
-->Rx=evstr(rep);
-->rep=x_matrix('y-noise covariance matrix',eye(ny,ny))
rep =
1.
-->if rep==[] then return,end
-->Ry=evstr(rep);
-->bigR=sysdiag(Rx,Ry);
-->[Plqg,r]=lqg2stan(P22,bigQ,bigR); //LQG pb as a standard problem
-->Klqg=lqg(Plqg,r); //LQG compensator
-->disp(spec(h_cl(Plqg,r,Klqg)),'closed loop eigenvalues:'); //Check internal stability
closed loop eigenvalues:
! - 4.9879273 !
! - 4.8577169 !
! - 0.6344970 !
! - 0.3472486 !
-->[Slqg,Rlqg,Tlqg]=sensi(P22,Klqg); //Sensitivity functions
-->disp(clean(ss2tf(Slqg)),'Sensitivity function');
Sensitivity function
2 3 4
- 42.573731 + 228.69605s - 120.71068s + 10.82739s + s
---------------------------------------------------
2 3 4
5.3385391 + 25.95691s + 34.116185s + 10.82739s + s
-->disp(clean(ss2tf(Tlqg)),'Complementary sensitivity function');
Complementary sensitivity function
2
47.91227 - 202.73914s + 154.82687s
--------------------------------------------------
2 3 4
5.3385391 + 25.95691s + 34.116185s + 10.82739s + s
-->
Closed-loop response