Chapter 4, lexical and syntactical analysis
Introduction
- Compiled
- Based
on formal description of language (BNF)
- Broken
down into different parts (see below)
- Interpreted
- Hybrid
- Java,
JVM
- Advantages
/ Disadvantages
The Language and its Compiler
A language is composed by the
following components:
- The front end
- The back end
A further definition would divide
the Front End into:
- The Language Grammar itself
- Lexical Analysis
- A Parser, sometimes called Syntactic
Analysis
- Semantic Analysis
And the Back End into:
- Code generation
- Eventually Optimization
We are only going to be worried
about the language’s front end at this
point.
Here is an overview of the
components used for the compilers front end:

The Grammatical Definition of a
Language
Before you get coding a compiler,
you need first to define the languages grammar.
Consider the following c++
assignment statement:
A = 8;
This statement could be
interpreted by our language in the following very simple manner:
<assignment> ::= ID = number ;
Where ID, =, and number are
called for “tokens”, which means the smallest portion of a language.
In this definition, we allow an
identifier to be assigned a number.
We state that an “assignment
statement” is composed of an identifier, followed by the “equal to” operator
(=), followed by a number, followed by a semicolon character.
<assignment> is a
non-terminant definition. This means that an assignment is composed of other
definitions.
ID and number are terminant
definitions, and they cannot be further defined. These tokens are called terminals.
A definition can be composed of
itself, like in a recursive algorithm. Examine the following definition:
< block > ::=
{ <sequence> }
< sequence > ::=
<statement> | <statement> ; <sequence>
This states: “A sequence is composed of a statement, or
a statement followed by semicolon followed by another sequence “. This definition
allows the language to have one or more statements within a block. A block is
surrounded by the { and } characters. Of course, the definition
upon still need to further define what a <statement> is composed of.
This BNF description we have discussed already, but now we
will find out what this definition is needed for.
Lexical
Analysis
Lexical analysis is the portion of the compilation process
which identifies and stores the symbols found in the source code file. The
compiler needs to know what in the source code is an identifier, a reserved
word, an operator, number or whatever the language possesses.
Whenever the compiler meets these symbols in the source
code, it needs to store them in a symbol description table, accordingly
with what type it is (numerical, string, identifier), together with other
relevant information about this symbol, such as its name, if it is an
identifier. (Page 164 in your book).
The compiler also needs to know the sequence in
which these symbols appear in the source code. This sequence could be stored in
a symbol sequence table.
Eventually could we put the languages reserved words
first in the symbol description table, and as the compiler meets identifiers
and numbers, place these last in the table. In the illustration bellow,
non-reserved symbols appear after symbol number 30.
 .
.
State Machine
A fairly elegant manner of solving the problem of
identifying the different symbols met in the source code is using a state
machine, reading the characters in the source code one by one.
A state machine is a machine that maps an event
to an action, and performs a state change. You
should recognize a version of a FSA.
For our purpose, the state machine would define:
·
An event to be whenever the compiler
meets a certain character,
·
An action to be what we do with that
character,
·
A state to be what step we are taking,
such as reading a number.
This is how states are illustrated in a state diagram:

Below is how an event together with a state change is
illustrated. If the compiler meets a letter in the source code, it changes its
state to “Reading
an identifier”, if the current state is “Reading whitespaces”. If the compiler
is currently reading an identifier, and then meets a space, then the state
machine changes its state to “Reading
whitespaces”:

The starting state for the state machine is marked
with a thick outline, whereas the ending state is marked with a double
outline.
Below is an example to a simple state machine for lexical
analysis, where the source code finishes with a point (.) character:
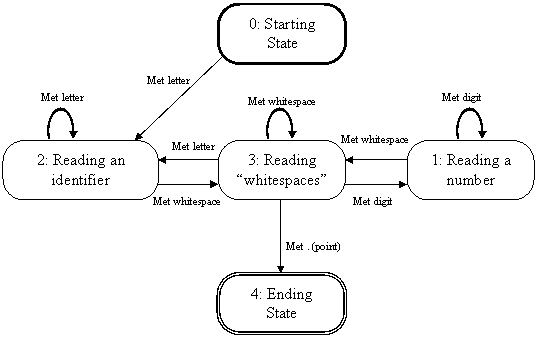
The above state diagram is simple, but also very strict.
For example, the source code must start with a letter, because according
to the state diagram, starting with another character is a lexical error.
A more relaxed approach would be to let the state 3
(whitespaces) be the starting state, thus allowing the source code to start
with a whitespace, digit, or letter.
Remark that a much more complex lexical analysis doesn’t
have to have many more states, just more events (arrows) mapped to each state.
Perhaps a standard c++ compiler has about 6-10 states in its lexical analyzer
(if it uses a state machine, of course). If the state diagram for a lexical
analyzer has too many states, it probably means that it could be better
structured, to fit a more compact structure.
Note also, that it is not the Lexical analyzers job
to check whenever a statement is illegal. This means that the following
statements should be legal a lexical check using the state diagram above:
t = x .
int A int int 5675 (
; .
Because they have legal characters, and follow a legal
path through the state diagram’s rules.
The following statements are not legal:
134GT = 32 .
§# * 5%;
Because a letter cannot immediately follow digits, and in
the second line there are illegal characters.
State Table
When the state diagram is defined, we just have to fill it
in an state table, so we can represent it in within the compiler.
A state table defines, which state the state machine is to
be switched to, upon a given event.
With other words, we can read the state table like: “If we
are at the starting state, and meet a letter, that we switch to state 2, which
is “reading an identifier” “. This means that the numbers in the middle of the
table are the number of the new state to be taken. See it in the table below.
The state diagram illustrated in the previous section
would be represented in a state table in the following manner:
|
|
Events
|
|
Met Letter
|
Met Whitespace
|
Met Digit
|
Met Point (.)
|
|
States
|
0
: Starting
|
2
|
5
|
5
|
5
|
|
1
: Number
|
5
|
3
|
1
|
5
|
|
2
: Identifier
|
2
|
3
|
5
|
5
|
|
3
: Whitespace
|
2
|
3
|
1
|
4
|
|
4
: Ending
|
4
|
4
|
4
|
4
|
|
5
: Error
|
5
|
5
|
5
|
5
|
The states are represented horizontally, while events
vertically. Note that state “Error” is include in the table, but not in the
state diagram. It is because we need to define a new state for every
event that can meet. This means that if we are in the middle of “reading
number”, and suddenly meet a letter, without any whitespaces, than this would
be considered as an lexical error.
Note that the lexical analyzer should stop processing as
soon as the current state of the state machine reaches 4 or 5, which correspondingly
means that the check is finished or ended with an error.
The state table is to be combined with the action table,
discussed in the next section.
Action Table
The action table specifies which action the compiler is to
take upon an event within a given state.
In other words: “What should the compiler do, if is
reading an identifier, and meets a whitespace?” – “It should put the identifier
in the Symbol description table”.
The numbers in the middle of the table refers to the
action number to be taken. The actions themselves are specified in a Action
List.
The two illustrations below are an example of two actions
and what they do with the source code, the symbol description table, and a
temporary symbol buffer.
Reading an identifier
Action : put the current character g in the symbol buffer.

Pushing Symbol
Finished with identifier (because we met whitespace),
reading whitespace.
Action : push symbol buffer in the symbol
description table (as an identifier), and clear symbol buffer.

Here is the Action List:
|
Number
|
Action
|
|
action 1
|
Ignore character, do
nothing.
|
|
action 2
|
Put character in the
symbol buffer.
|
|
action 3
|
Push symbol buffer to
the Symbol Description Table as an identifier, then clear buffer.
|
|
action 4
|
Same as action 3,
just push as a number.
|
|
action 5
|
Push character
directly to SDT, without using the buffer.
|
|
action 6
|
Show an appropriate error
message.
|
And finally, the Action Table itself:
|
|
Events
|
|
Met Letter
|
Met Whitespace
|
Met Digit
|
Met Point (.)
|
|
States
|
0
: Starting
|
a2
|
a6
|
a6
|
a6
|
|
1
: Number
|
a6
|
a4
|
a2
|
a6
|
|
2
: Identifier
|
a2
|
a3
|
a6
|
a6
|
|
3
: Whitespace
|
a2
|
a1
|
a2
|
a5
|
|
4
: Ending
|
a1
|
a1
|
a1
|
a1
|
|
5
: Error
|
a6
|
a6
|
a6
|
a6
|
Consider for example, that the compiler is reading a
number (state 1), and it meets a whitespace. Action 4 pushes what currently digits
are in the buffer to the symbol description table as a number - symbol. This is
exactly what we want to happen.
The Parser
The parser’s job is to ensure that the symbols have a
legal sequence, as defined in the languages grammatical syntax. This process is
sometimes also called Syntactic Analysis.
Actually, a parser can be built very simply, if the
language allows it to be. The parser can be constructed using recursion.
For accomplishing its task, the parser needs both the symbol
description table and the symbol sequence table.
The first because it needs to know what the current symbol
is, whatever it is a specific reserved word, an identifier, number or whatever.
The second because it also needs to check the sequence of
these symbols against a matching valid pattern, and this pattern is what the language
grammatical definition specifies.
There are a few steps, which can greatly simplify the
construction of a parser, here are the rules:

For the above rules to work, it is required that the
Symbol description table has methods to retrieve the following information
about a symbol:

Here is an example:
Language’s syntax definition:
This language can only make assignments to identifiers,
and perform input/output.
Here is the parser for the language, with the rules
applied in the § boxes:
int symbolcounter
= 0;
bool CheckReservedWord ( char* SymbolString )
{
if ( SymbolString
== SymbDescTab[ SymbSeqTab [symbolcounter] ].GetName()
)
{
 symbolcounter ++;
symbolcounter ++;
return
true;
}
else
return
false;
}

bool IsSymbolIdentifier ( )
{
if ( SymbDescTab[
SymbSeqTab [symbolcounter] ].IsIdentifier() )
{
symbolcounter
++;
return
true;
}
else
return
false;
}
bool IsSymbolNumber ( )
{
if ( SymbDescTab[
SymbSeqTab [symbolcounter] ].IsNumber() )
{
 symbolcounter ++;
symbolcounter ++;
return
true;
}
else
 return false;
return false;
}
bool Program
( )
{
// <program> ::=
begin <sequence> end.
if ( ! CheckReservedWord
(“begin”) )
return
false;
if ( ! Sequence()
)
return
false;
if ( ! CheckReservedWord
(“end”) )
return
false;
if ( ! CheckReservedWord
(“.”) )
return
false;
return
true;
}
bool Sequence
( )
{
// <sequence> ::= <statement> | <statement> ; <sequence>
if ( ! Statement()
)
return
false;
if ( CheckReservedWord
(“;”) )
{
if ( Sequence
() )
return true;
}
return
true;
}
bool
Statement ( )
{
// <statement> ::= <assignment> | <io>
if ( Assignment()
)
return
true;
if ( Io()
)
return
true;
return
false;
}
bool
Assignment ( )
{
// <assignment> ::= ID = number
if ( ! IsSymbolIdentifier
() )
return
false;
if ( ! CheckReservedWord
(“=”) )
return
false;
if ( ! IsSymbolNumber
() )
return
false;
return
true;
}
bool Io ( )
{
// <io> ::= <output> | <input>
if ( Output()
)
return
true;
if ( Input()
)
return
true;
return
false;
}
bool Output (
)
{
// <output> ::= out ID , number
if ( ! CheckReservedWord
(“out”)
return false;
if ( ! IsSymbolIdentifier
() )
return
false;
if ( ! CheckReservedWord
(“,”)
return
false;
if ( ! IsSymbolNumber
() )
return
false;
return
true;
}
bool Input (
)
{
// <input> ::= in ID , number
if ( ! CheckReservedWord
(“in”)
return
false;
if ( ! IsSymbolIdentifier
() )
return
false;
if ( ! CheckReservedWord
(“,”)
return
false;
if ( ! IsSymbolNumber
() )
return
false;
return
true;
}
The return value of the function “bool Program( )” will
give the result of the syntactic analysis.
At this point of the compilation process, the compiler can
assume that the source code is ready to analyze the semantics of the code, this
will be discussed next.
Semantic Analysis
The task of this compilation part, is to ensure that the
identifiers referenced in the source code are valid, check that you cannot
assign two identifiers of different types (for example assigning a string value
to an int variable).
My first bet would be to create a structure or class for
each relevant language definition.
For example, we need an structure to hold information
about an <input> statement. If you recall, this statement is defined as:
<input> ::= in ID , number
The information needed to be hold are:
·
ID, the identifiers name.
·
Number. It’s value.
We could define a class:
class InputStatement
{
public:
void
Define_Identifier (int Symbolnumber );
void
Define_Number (int Symbolnumber );
bool
Check_Semantics ( );
private:
int Identifier_SymbolNumber;
int NumberValue_SymbolNumber;
}
The parser would then fill this structure in the
appropriate function: bool Input ( ) ; using the methods “Define_Identifier()“
and “Define_Number()”
as these are met. If the statement was not an “Input” statement at all, the
parser method would then just throw this structure away.
In the case of a c++ language, the “Check_Semantics ( )”
method would check if the identifier is already declared, and if number is in a
legal port number. To check if a identifier (variable) is declared, the Symbol
description table would need, along other information, reserve a field to mark
if this identifier were previously declared. We would also need a definition,
that could declare a variables type. Something like in c++’s “long var1 = 8;”.
The process of semantic analysis is actually very distinct
from language to language. It can be very time consuming and processor
extensive, but the real difficult part is setting up the semantic rules.

 .
.