CS430 - S'05
Lecture 01 : 1/13/05

Reading Assignment: Chapter 1 & 2 Gonzalez/Woods

Today's Topics

• Course Overview
• Images (continuous & discrete)
• Sampling and Quantization

"Peppy" the cat.

• Course Overview
• General Information
• Lectures
• Processing assignments.
• Gimp
• CVIPtools
• Adobe Photoshop
• Hard copy
• Programming assignments.
• Gimp plug-ins
• CVIPlab
• pgm in/out and viewer (Linux: xv)
• Hard copy
• Spot Check Demos
• Homework
• Exams
• Online References
• Images
• What do you see?
• 180° wide by 90° high
• 10 feet radius
• ~ 1/4 surface area of a sphere
• ~ 1000 square feet
• 1000 bits/inch => 1,000,000 bits/sqare inch
• 144 square inches / square foot => 144 Mb/sq.ft.
• 144,000 Mb
• Limited resolution (high at fovea, low outside)
• Optic nerve pre-processing
• Brain Processing
• Resolution of the human eye.
• Continuous Image f(x,y)
• f(x,y) = i(x,y)r(x,y)
• i(x,y) is illumination
• theoretical: 0 <= i(x,y) <= infinity
• practical: full moon (0.1 lm/m²) bright sun (90,000 lm/m²)
• r(x,y) is reflectance
• theoretical: 0 <= r(x,y) <= 1
• practical: black velvet (0.01) snow (0.93)
• Discrete Image f(x0,y0)
• Intensity of monochrome image at any coordinates (x0,y0) is called "gray level" of the image at that point. L = f(x0,y0)
• L(min) <= L <= L(max)
• L(min) = I(min)*R(min)
• L(max) = I(max)*R(max)
• Assume indoor lighting, L(min) apx. 10, L(max) apx. 1000
• [L(min),L(max)] gray scale, normally shifted [0,L-1]
• L is number of gray levels
• 0 = black
• L-1 = white
• Need to represent L as an integer (see Table 2.1, note: bits!)
• Peppy is 512 x 512 x 256 (8 bits) or 262,144 bytes
• Limitations of our computer equipment
• A Good Image??? (We have a GREAT image evaluator system.)
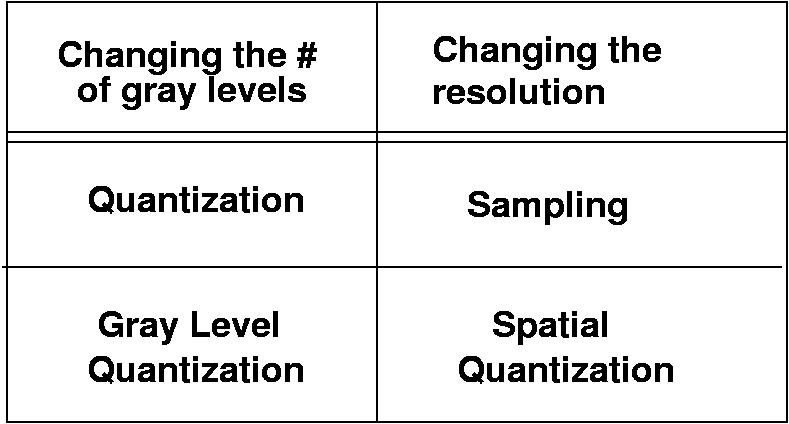
• Sampling/Quantization Pre-Quiz

• 

• Quantization Example

• Sampling and Quantization Example

• Sampling Example


• Spatial Quantization (fig 2.19 & 2.20)
• Gray Level Quantization (fig 2.21 & 2.22)
• Magnification Example
• Example 2