Contaminant Bioremediation: Session II-3

Session II-3. Microbial Process Kinetics

The kinetics of dissolved contaminant biodegradation are discussed in chapter 4 Wiedemeier, section 4.4 pages 178-186. There are three mathematical models used to describe biodegradation kinetics:

Zero order (i.e. biodegradation rate is constant with time).

First order (i.e. biodegradation rate is directly proportional to dissolved contaminant concentration).

Monod kinetics.

These three kinetic expressions are discussed in section 4.4. Assignments using the BIOSCREEN model will provide additional background on biodegradation kinetic concepts. Begin by reading the following 4-page tutorial, entitled “Microbial Kinetics”, which describes how the Monod kinetics growth curve is is developed in well-mixed batch reactors in the laboratory. The relationship between “Monod kinetics”, and “zero” and “first order” kinetics is subsequently explained.

Microbial Kinetics

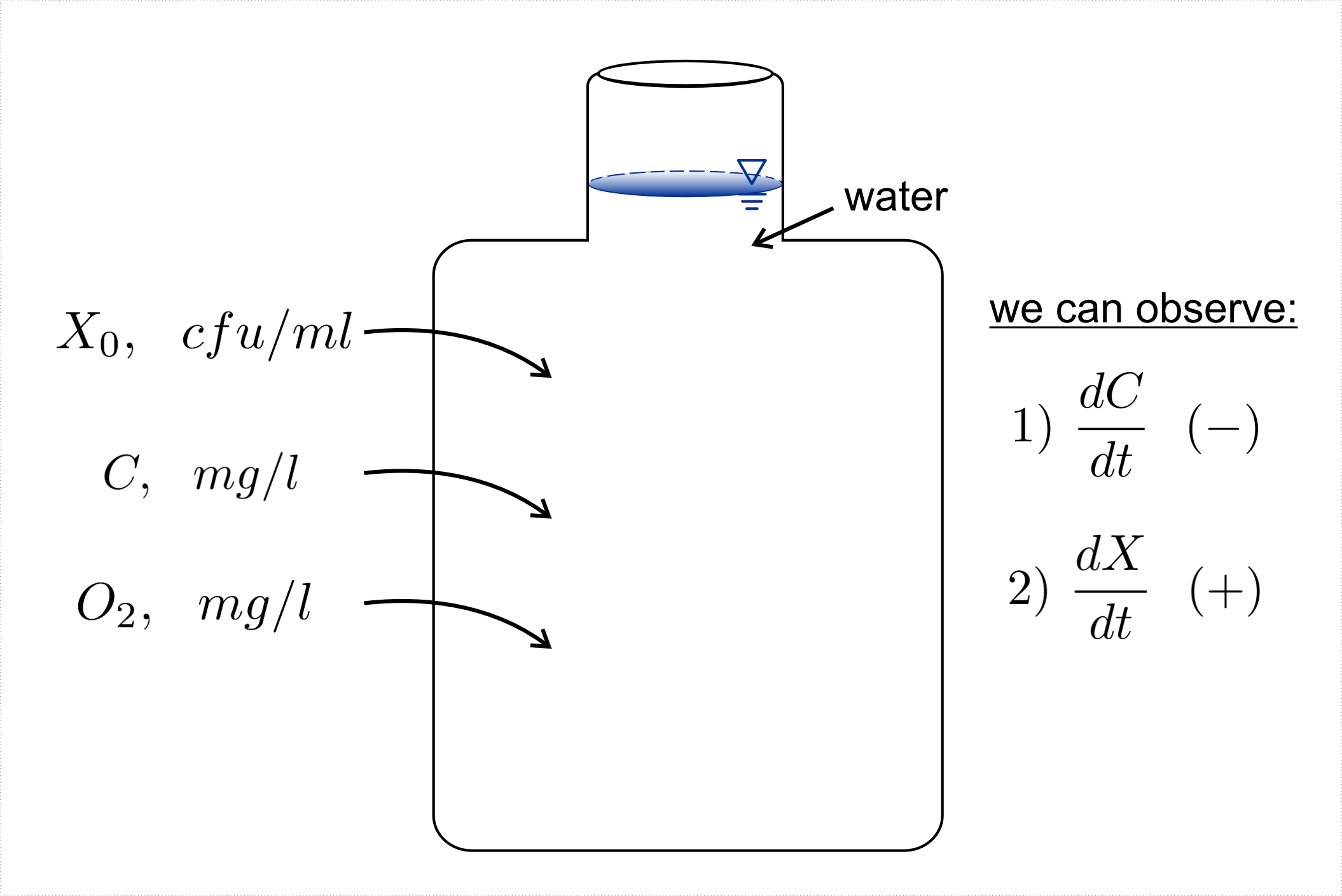
Known concentrations of Oxygen (O2,mg/l), primary growth substrate (C,mg/l), and microbial inoculum (X0, cfu/l) are added to a well stirred container of water (Figure II-12). Microbial activity begins converting substrate into more microbial cells (biomass).

Figure II-12

Figure II-12. Biodegradation in a well-mixed container

With these Observations, we can compute:

1. Yield coefficient * :

$Y = \frac{d X}{d S} = \frac{mass of new cells}{mass of substrate consumed}, [dimensionless]$

S = total Mass of Substrate consumed during interval dt
* Note: Y is sometimes called the 'substrate-to-biomass yield'

2. Specific growth rate:

$μ = \frac{d X}{X_{0} d t} = \frac{mass of cells produced}{original mass of cells \cdot time}, [\frac{1}{time}]$

It follows that:

$\frac{d X}{d t} = μ X_{0}$

$\frac{d C}{d t} = \frac{d X}{Y d t} = \frac{μ X}{Y}$

where “X” is biomass concentration at any arbitary time “t”.

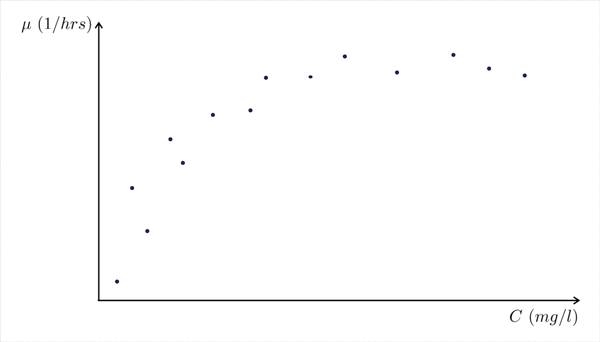
Now, if we repeat this procedure, keeping O2 and X0 constant but changing substrate concentration “C” over a wide range of values, we will generate a “μ” value corresponding to each C value and we can make the following graph (Figure II-13):

Figure II-13

Figure II-13. Specific Growth Rate vs. Substrate Concentration

Each point on the graph represents the “μ” value observed for a particular substrate concentration in the flask.

Monod Kinetics

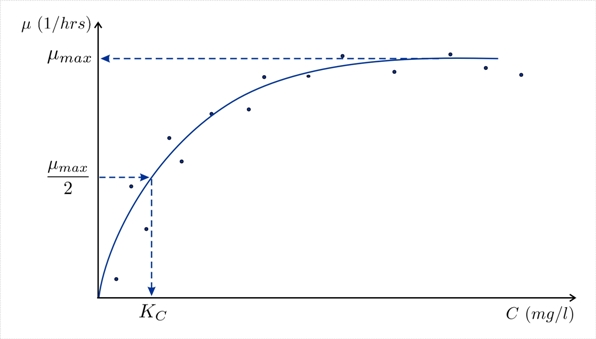
To obtain Monod Kinetic parameters, we first fit the Monod saturation equation through the data in Figure II-13. This saturation equation is:

$μ = μ_{m a x} (\frac{C}{C + K_{C}})$

Figure II-14. Monod Kinetics Graph

From Figure II-14 we see that μmax is equal to the maximum specific growth rate observed. KC is seen to be the substrate concentration corresponding to $\frac{μ_{\max}}{2}$ .

Based on the Monod Saturation relationship we have:

$μ = μ_{m a x} (\frac{C}{C + K_{C}})$

$\frac{d X}{d t} = μ X_{0} = μ_{m a x} X_{0} (\frac{C}{C + K_{C}})$

$\underset{\begin{array}{l} Monod Equation for Contaminant Biotransformation Rate \end{array}}{\frac{d C}{d t} = \frac{μ X}{Y} = \frac{μ_{m a x} X_{0}}{Y} (\frac{C}{C + K_{C}})}$

Zero Order Kinetics>

From the Monod Equation for Contaminant Biotransformation Rate (and Figure II-13) we see that if C >> KC:

$\frac{d C}{d t} = \frac{X_{0} μ_{m a x}}{Y} (= constant)$

First Order Kinetics

From the Monod Equation for Contaminant Biotransformation Rate (and Figure II-13) we see that if C << KC :

$\frac{d C}{d t} = (\frac{X_{0} μ_{m a x}}{Y K_{C}}) C = K_{b} C$

where “Kb ” is defined as the first order biodegradation rate coefficient.

Written Assignment: Questions II-7 through II-11.

Next Session