Formal Definition of an FSA

< Previous

Page 6 of 8

Next >

Formal Definition of a Finite State Automaton

At some point we can't rely on good old English to describe any model of computation we might dream up, including finite state automata. Why? Well, English is inherently ambiguous. It is almost impossible to write a definition in English of anything that is at least moderately complex so that there is only one way to understand what the definition means. That's one of the reasons lawyers get such a bad rap--legal language is pretty hard to wade through just because it represents an attempt to express laws in a way such that a given law has only one interpretation. Alas, this venture is doomed to failure, which is why cases are routinely brought to the Supreme Court of the United States that require an opinion about what various provisions in the Constitution of the United States mean. What do free speach, separation of church and state, freedom of the press, and other such provisions of the Constitution really mean?

But enough of politics for a while.

To ensure that this same sort of ambiguity does not happen to us in the theory of computing, we resort to precise mathematical expressions, rather than English prose, for describing the objects that we are trying to study. At first (and, for some of us, maybe even at last) the language of mathematics looks intimidating and virtually undecipherable. But once you warm up to it, it's clarity is comforting.

Let's try to get to a definition of finite state automata. In getting to this point, we first looked at a number of examples of finite state automata. Then we tried to capture in English what we saw. Paraphrased, this is what we said first about an FSA:

What parts can we identify in any FSA?

There are circles. The circles represent the states of the FSA.

One of the states (circles) is marked by a special ">" symbol. This is the start state of the FSA. Every time the FSA begins processing a new input string it starts doing so in this special start state.

Some of the states are represented by a double circle. This type of state is referred to as an "accepting state." If, after the FSA has finished processing all of the symbols on its input tape, it is found in a double-circle accepting state, we say that the input string was accepted, otherwise we say that the input string was rejected.

There are labeled arrows leading from one state to another (sometimes leading to the same state). We call these all of these labels on the arrows, taken together, the input symbols of the FSA

We call the labeled arrows themselves transitions, becuase they show how the FSA transitions from one state to another on a particular input symbol. That is, the current state of the FSA and the current input symobl being processed uniquely determine the next state of the FSA.

This description of an FSA was way too vague and too verbose, so we made it simpler by shortening it thus:

The parts of an FSA are:

A set of states

A designated start state from among the set of states

A designated set of accepting states

A set of input symbols

A set of transitions between states

Even this shorter English description is not satisfactory. We don't know from this description, for example, whether the set of states must be finite. So we finally give up on English and attempt a precise mathematical definition.

Definition, Try 1

A finite state automaton (FSA) M = (S, s₀, A, I, T) is a mathematical model of computation with five components, where

S is finite set of states
s₀, is the designated start state in S
A is the subset of accepting states in S
I is a finite set of input symbols
T is a transition function T: S×I → S □

Notice that this is precise. It also requires that you remember certain kinds of mathematical notation. For example, what does

T: S×I → S

mean? The × is our old friend, Cartesian product, that we probably last saw a good while ago now. This line just says in very precise mathematical terms that T is a function, T(s,i) = r, that takes as parameters any state s in S and any input symbol i in I and returns a state r in S. That is, this is just a mathematically precise way to state that an FSA must have a scheme that tells the reader how the FSA changes states based on the current state and current input symbol.

Given any FSA M defined as above, you could easily construct the graphical representation of M and vice versa: given any completely specified FSA M in graph form you could easily list the componets S, I, T, s₀, and A of M.

Oh, and by the way, why did we use M to stand generically for an FSA? Tradition. FSA's are often referred to as finite state machines. Hence the M.

Speaking of tradition, we are going to bow to it now and give you a final definition of a finite state automaton. We don't particularly like it, but tradition does have some benefits in that they keep a link to past practices. So if you read a book or article on FSA's elsewhere, you are more likey to see an FSA expressed in these terms. This is all just notation. No big deal, but here it is.

Definition (the Real One)

A finite state automaton is a mathematical object with five conponents, M = (Q, Σ, δ, q₀, F), where

Q is a finite set of states
Σ is a finite set of input symbols
δ: Q×Σ →Q is a total function (called the transition function)
q₀∈Σ is the start state
F ⊆ Q is the set of accepting states. □

We might have these questions about this traditional definition:

Why name the state set Q? Dunno. Would that be a good, descriptive variable name for states in a programming language? Nope. Give up guessing; it's just tradition.

Why name the input symbol set Σ? Two reasons, probably. Mathematicians just don't feel whole if they don't use Greek symbols occasionally. Furthermore. Σ is the capital Greek letter Sigma, which starts with an "s" sound, which might invoke "symbols" in your mind. (Did you get that?)

Why use δ for the transition function? It's that Greek thing again, plus the fact that δ (delta) has been used since time immorial to stand for a "small change" of some sort. Here δ is used to describe how the FSA M changes states.

Why list q₀ for the start state? Well, this at least makes a bit of sense. Since the set of states is Q there is some continuity in naming the states in Q genericaly as q with some subscript.

Why F? In some literature the set F is called the set of final states rather than accepting states. Such states are not necessarily final in that the FSA may reach such a state during processing and then continue on to other states. Perhaps it is best to think of it this way: If, after an FSA has finally finished processing an input string, it halts in a state in F then it accepts the input string.

Finally, why is the FSA definition ordered this way, so that the start state q₀ does not appear right after the set of states Q is specified? Who cares.

Whatever. Like we said, it is all a matter of traditional mathematical notation. Like the rest of us, you'll just have to deal with it.

A finite state automaton M functions as follows:

M is supplied an input string w ∈ $Σ^{*}$ to process, where w = $a_{1} a_{2}$ ... $a_{n}$ , each $a_{i}$ ∈ Σ, and n ≥ 0 (for n = 0, x is the empty string, λ).
M begins its processing of w in state $q_{0}$ .
M performs n operations, or steps, on the input string w, one for each of the n symbols in w.
If n = 0 (x = λ), M simply halts in state $q_{0}$ without performing any operations. If n > 0 (w ≠ λ), M processes each symbol in w in succession according to the transition function, each step in the processing of w yielding a new state. Step 1 would result in a state $q_{1}$ determined by applying the transition function to the start state $q_{0}$ and the first symbol of $a_{1}$ of w (that is, δ( $q_{0}$ , $a_{1}$ ) = $q_{1}$ ), step 2 would result in a state $q_{2}$ determinied by applying the transition function to $q_{1}$ and $a_{2}$ (that is, δ( $q_{1}$ , $a_{2}$ ) = $q_{2}$ ), and so forth.

Upon completion of processing of w, M will be in some state $q_{n}$ . If $q_{n}$ is in F, M accepts w; otherwise M rejects w.

Of course, a finite state automaton is really not an operational computer but rather just a mathematical model, a total function M: $Σ^{*}$ → {accept, reject}.

1.2 Graphical Representations of Finite State Automata

Although the formal definition captures the mathematical essence of a finite state automaton, it is notoriously difficult to discern what a finite state automaton computes from the definition alone. As a result, finite state automata are traditionally illustrated as directed, labeled graphs, which provide a much more intuitive mental model of their function. The nodes of the graph represent the states, Q, of the automaton. The directed, labeled edges represent the transition function, δ; there is an edge from state s to state p labeled with a in the graph of M if and only if δ(s, a) = p. The start state is marked with the > symbol, and accepting states are indicated by nodes depicted as double circles.

Example 1.1

Consider the following finite state automaton M presented in graphical form.

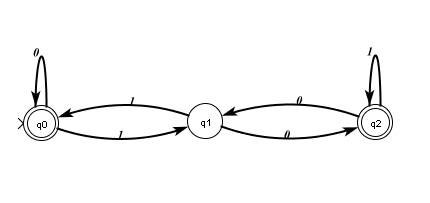
From this graph we can deduce the formal definition of M. M = (Q, Σ, δ, q₀, F) is a finite state automaton where

Q = { $q_{0}$ , $q_{1}$ , $q_{2}$ }
Σ = {0, 1}
F = { $q_{0}$ , $q_{2}$ }
δ( $q_{0}$ , 0) = $q_{0}$ , δ( $q_{0}$ , 1) = $q_{1}$ , δ( $q_{1}$ , 0) = $q_{2}$ , δ( $q_{1}$ , 1) = $q_{0}$ , δ( $q_{2}$ , 0) = $q_{1}$ , δ( $q_{2}$ , 1) = $q_{2 .}$ □

As you can see, the graphical version of the FSA M is much easier to get a handle on than the formal mathematical definition. However, it is easy to build an FSA from its formal definition, and a formal definition serves other purposes as well. It is the benchmark against which we can mathematically determine whether a proposed language can be recognized by an FSA or not. We will explore this later.

Chapters

The Theory of Computing

Finite State Automata, Rebular Languages, and Regular Expressions

Pushdown Automata and Context Free Languages

Sections

Where We Are