Regular Grammar Assignment 1

This assignment is to help familiarize you with regular grammars and regular languages.  Questions asked here are answered in the hypertextbook, chapter 2, section 5.

We will use the following grammar in much of the assignment.  Let G = (N, Σ, P, S) be a regular language that has the rules

P = { S → a S
         S → b S
         S → c A
         A → a A
         A → b A
         A → c B
         B → a B
         B → b B
         B → c B
         B → ε }

1.  Give, in true set notation, the set N as inferred from this set of rules.
   
   
   
   
2.  Give, in true set notation, the set Σ, as inferred from this set of rules.
   
   
   
   
3. Describe what each of the following arrow notations are used for.
   
   →
   
   
   
   
   ⇒
   
   
   
   
   
   $\stackrel{k}{\Rightarrow }$
   
   
   
   
   $\stackrel{*}{\Rightarrow }$
   
   
   
   
   
   
   
   
4.   Give a derivation in "one step at a time drivation steps" of the string abacabc in this grammar.  Be sure to use the correct arrow notation.
   
   
   
   
   
   
5. Give the same derivation using parse tree notation.
   
   
   
   
   
   
   
   
   
   
   
   
   
6. Build a finite state automaton from the given grammar that recognizes the same language.  Don't just build an FSA that recognizes the same language, but rather try to determine an algorithm that can turn a regular grammar into an equivalent FSA.  You don't need to describe the algorithm, but your FSA should indicate that you know how the algorithm would work (hint:  name the states of your FSA with the nonterminal names).
   
   
   
   
   
   
   
   
   
   
7. Given the following FSA, create a regular grammar from it in the spirit of problem 6.
   
   
   
   
   
   
   
   
   
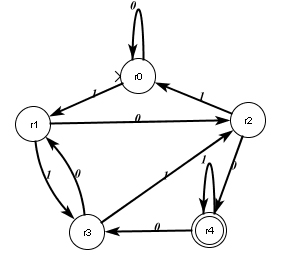
8. State and prove the pumping lemma for regular languages. Use the same pumping lemma found in Sipser, but prove it based on regular grammars rather than finite state automata.