Regular Grammars: A First Look
As if we did not have enough of regular languages already, we introduce one final (we promise) formal specification for regular languages: regular grammars. Every regular language can be specified by a finite state automaton, a regular expression, or a regular grammar. Furthermore, all of these specifications are equivalent in the sense that they all capture the class of regular languages.
Each of these different formalisms for regular languages serves a different purpose, as summarized in the table below.
| Finite State Automaton | Recognizer | Determines whether a particular input string is in the regular language recognized by the FSA or not. |
| Regular Expression | Expresser | Expresses a regular language as a pattern to which every string in the regular langauge conforms. |
| Regular Grammar | Generator | Provides grammar rules for generating strings in the regular language |
So what is a regular grammar? As the table indicates, it is a formal specification of a regular language by way of grammar rules.
Example of a Regular Grammar for Generating all Binary Strings that End in 101
We already know that the set of all binary strings that end in 101 is a regular language. An FSA for this regular language is
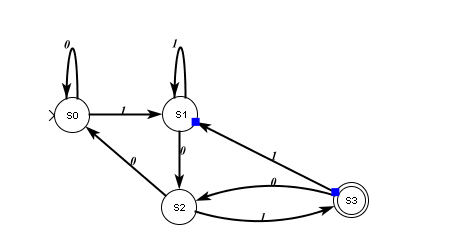
A regular expression for this language is
(1 | 0)* 101
A list of regular grammar rules for generating all binary strings that end in 101 is
1. S → 0S
2. S → 1S
3. S → 1A
4. A → 0B
5. B → 1
The way we use these rules is to start with the start symbol for the grammar, in this case S, and apply rules. We can only apply rules 1-5 to the symbols that appear on the left of the →'s in the grammar rules . When we wind up with a string of all 1's and 0's, we have a string in the language of this grammar. So, the following derivation,
S ⇒ 0S ⇒ 01S ⇒ 011S ⇒ 0110S ⇒ 01101A ⇒ 011010B ⇒ 0110101
shows that the string 0110101 is in the language generated by these grammar rules.
Some things to notice on first glance:
- Capital letters (S, A, and B) are used to stand for special grammar symbols to which rules can be applied.
- The other symbols (0 and 1 in this example) are symbols from the alphabet of the language the grammar describes.
- The single right arrow, →, is used for describing rules.
- A derivation shows how one string is derived from another by application of rules in the grammar.
- The double right arrow, ⇒, is used for a sigle step in a derivation, in which just one rule is applied.
So we can say that the string S derives the string 0S, S ⇒ 0S by applying rule 1, S → 0S to S. S also derives the string 01S by first applying rule 1 to S to get to 0S and then applying rule 2 to the S in 0S to get to 01S, and so forth. By continuously applying various rules to the capital letter in a string we can show that S derives 0110101. □
Example of a Showing that a String is Generated by a Regular Grammar by Way of a Parse Tree.
Another way to illustrate that a string is in the language generated by some regular grammar is to build a parse tree in which the interior nodes are the symbols that appear on the left of the → in the grammar rules, and the leaves are the other symbols. A parse tree for the string 0110101 from the grammar of the previous example is
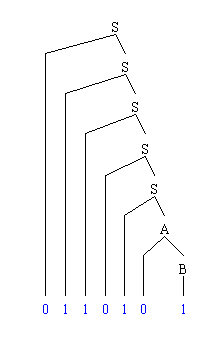 □
□
A Visual Example
Try your hand at buiding parse trees for the grammar of the the above two examples in the regular grammar applet given below. Be sure to read the user's guide under the Instructions tab first. There are two things especially to note. You can run the applet in either the parse tree mode or the derivation mode, by selecting either the Parse Tree Pane or the String History Pane. Try them both. Also, convince yourself that this grammar not only generates all binary strings that end in 101, but also that it does not generate any other binary strings. Also, to expand a rule, you must click on the nonterminal to expand in the lower pane. It will turn red. Then you must click on the rule you want to apply to that nonterminal in the upper pane. Finally, you must click the Expand button. There are also options for undoing what you have done at any step in order to retry a different approach.


