Ambiguity
Here is an interesting grammar. It generates all of the usual arithmetic expressions similar to the grammar on the previous page, but it looks different.
- Expression → Expression + Expression
- Expression → Expression - Expression
- Expression → Expression * Expression
- Expression → Expression / Expression
- Expression → identifier
- Expression → integer_literal
- Expression → ( Expression )
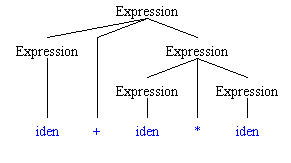
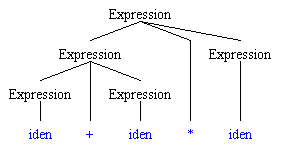
One interesting thing about this grammar is that it allows for two different ways of parsing this string:
identifier + identifier * identifier
which corresponds to an arithmetic expression such as
a + fred * jack.
The following two parse trees illustrate this fact.
The parse tree on the left seems to be better at representing normal operator prescedence. It appears that the multiply would be done before the add, as we would expect. The parse tree on the right seems to indicate that the add should bd done before the multiply.
For practical applications we don't like this kind of ambiguity.
Definition
A context free grammar G is ambiguous if there is at least one string w in L(G) for which there are at least two different parse trees for w in G.
Example: A Different Grammar for Arithmetic Expressions
In the context free grammar applet below select the grammar that most looks like the one above:
- click on Access Grammar Tools Menu
- click on select a different grammar from menu
- select Arithmetic Expr #1
Build as many different parse trees as you can for the arithmetic expression:
a * (b + c) / 3
where, again, a, b, and c are identifiers and 3 is an integer literal.