The Parts of a Finite State Automaton
Let's look at our even parity FSA from the previous page again. Here it is.
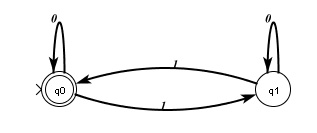
An FSA that solves the Even Parity problem
What parts can we identify?
- There are circles. The circles represent the states of the FSA. This FSA has two states. We label states to make it easier to refer to them. In this example, the states are labeled q0 and q1, respectively .
- One of the states (circles) is marked by a special ">" symbol. This is the start state of the FSA. Every time the FSA begins processing a new input string it starts doing so in this special start state.
- One of the states is represented by a double circle. This type of state is referred to as an "accepting state." If, after the FSA has finished processing all of the symbols on its input tape, it is found in a double-circle accepting states, we say that the input string was accepted, otherwise we say that the input string was rejected.
- There are labeled arrows leading from one state to another (sometimes leading to the same state). We call these arrows transitions, becuase they show how the FSA transitions from one state to another on a particular input symbol. That is, the current state of the FSA and the current input symobl being processed uniquely determine the next state of the FSA.
- As noted, the arrows have labels on them. We call these all of these labels taken together the input symbols of the FSA.
Thus, we can say that a finite state automaton has five parts:
- A set of states
- A designated start state from the set of states
- A designated set of accepting states
- A set of transitions between states
- A set of input symbols
Remember that we said that anything we would call a solution to a problem would itself have to be finite. So all five of these parts of any finite state automaton must be finite. Further note that this even parity FSA, even though it is finite, can correctly determine for any one of an infinite number of input strings whether that string has an even number of 1's or not.
What do the States of a Finite State Automaton Represent?
What exactly do we mean by the word "state" in a finite state automaton? Alaska? A state of mind? A state of being?
Glad you asked. State of being comes closest. That is, the states of an FSA represent what the FSA remembers about what it has encountered so far in processing an input string on the way to accepting or rejecting the string. Look at the even parity FSA again.
This time let your mouse hover over each of the states briefly. You will notice that a short description pops up that indicates what the state remembers. This description is nothing more than a comment, similar to a comment you would include in a regular program to indicate the state of processing at the point of the comment. So, although we use short names, like q0, to identify states, when designing an FSA to solve a particular problem, we need to keep in mind just what it is that we know about the computation so far at each state. It helps to include comments in the design for this purpose.
In fact, good comments for a state really help both to design and to prove the correctness of the design. Notice that the comment for state q0 is "have processed an even number of 1's so far." This helps us realize that this state should indeed be an accepting state, because if the FSA runs out of input while in this state then the string processed contained an even number of 1's. It also helps us know that if the FSA encounters a 1 in the input while in state q0 it no longer has processed an even number of 1s, but rather an odd number, so it should transition to a state that remembers this state of the computation. The comment associated with q1 indicates this fact.


