Our Second Finite State Automaton
Let's look at another simple finite state automaton. Before we do, let's remember our first FSA, the one that solves the Even Parity decision problem. Here it is again.
An FSA that solves the Even Parity problem
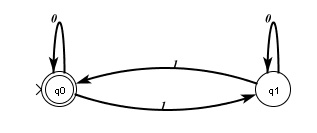
Take a good look at it, and then compare it with the new FSA below.
Do you see a difference? The accepting state and non-accepting states have been swapped. In the even parity FSA the start state, q0, is the accepting state. In this one, q1 is the accepting state. The transitions and start state are the same.
Given this difference what set of binary strings would you expect this FSA to recognize? This one will accept all of the strings that the even parity FSA rejects, and reject all of the strings that the even parity FSA accepts. That is, since the even parity FSA accepts just those strings that have an even number of 1s, this new FSA accepts just those strings that have an odd number of 1s (i.e., all binary strings of odd parity).
We can define the problem that this new FSA solves this way.
Definition. Odd Parity is this decision problem:
Given a binary string x, does x contain an odd number of 1s?
OK, we admit it. This new FSA is really not all that exciting. However, it does show that if we have an FSA that solves a particular decision problem we can easily build an FSA that solves the opposite (complementary) decision problem: we just create a new FSA just like the first except that the accepting states of the first become non-accepting states in the second, and vice versa.
We'll look at a few more FSA's that are a bit more exciting, and then we'll have you try some on your own.


